Can we estimate diversification rates on extant phylogenies?

01 Aug 2019

An exciting new paper by Stilianos Louca and Matt Pennell, “Extant timetrees are consistent with a myriad of diversification histories”¹, is out now in Nature. I think it’s an interesting paper and wanted to quickly jot down my thoughts on it.

There’s been widespread use of software tools like BAMM, RPANDA, and SSE-class models to estimate how diversity is generated by varying diversification rates. The huge amount of attention on papers that highlight where our blind spots could be when estimating rates² indicate that the field really cares about getting this stuff right, because it has important implications for all of our downstream analyses.

Nee et al. 1994³ showed that you could estimate speciation and extinction rates on an extant-only phylogeny by fitting two separate rates to a lineage-through-time plot (left panel). However, when rates are variable, it becomes impossible to identify whether there are, for example, two separate speciation rates, one older and one newer, or whether there is high extinction towards the present (right panel).⁴

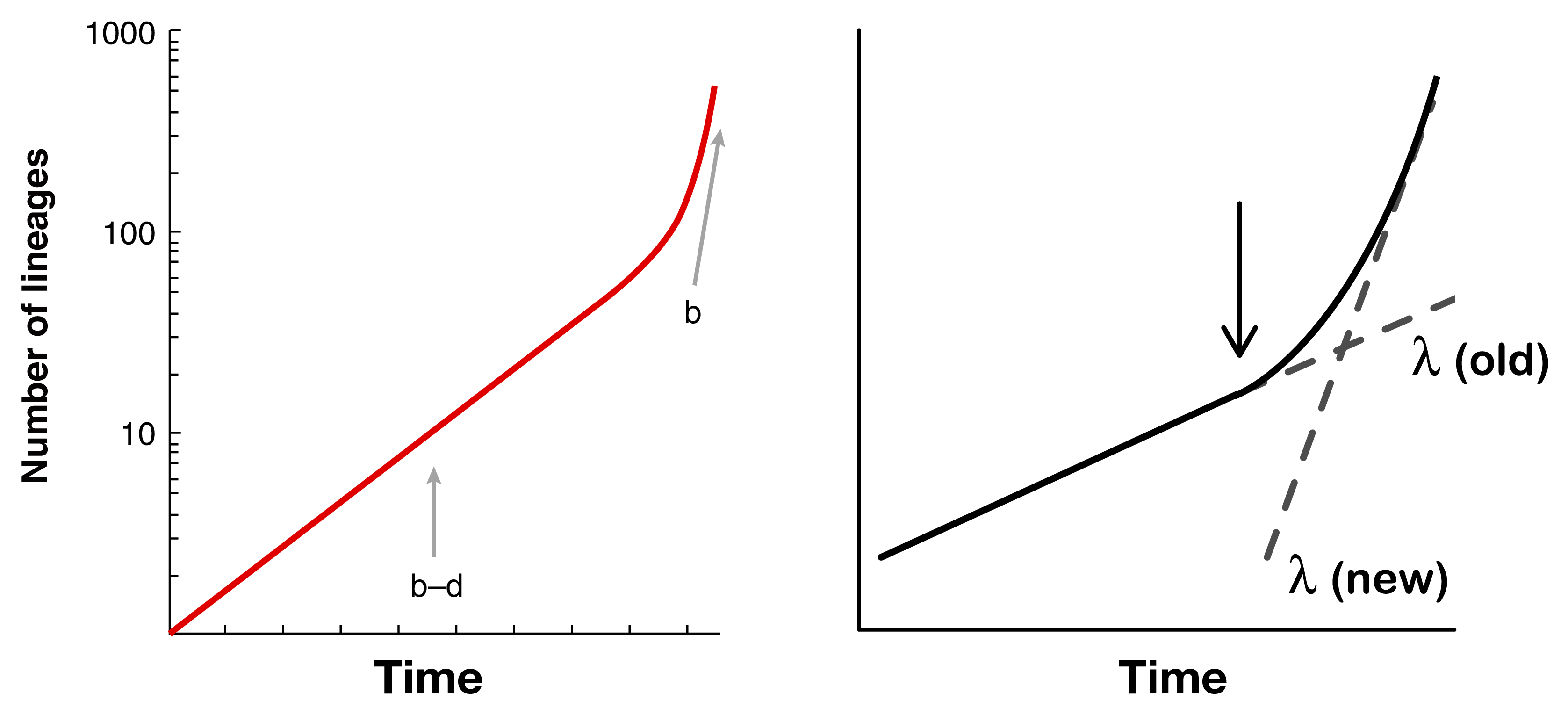
Dealing with these kinds of non-identifiability issues is really critical when fitting rate-varying diversification models. For example, with incompletely sampled phylogenies, you need to know either the amount of incomplete sampling or the extinction rate, otherwise these are non-identifiable.⁵ A paper that I co-authored also found that when both speciation and extinction are allowed to vary, model fit suffers substantially, likely due to identifiability problems, and our estimates of diversification rates can therefore vary wildly.⁶

Louca and Pennell unify the findings of these (and other) previous works and show that for any extant phylogeny, where (potentially time-varying) speciation and extinction rates have been fit, you can construct an infinite number of alternative speciation and extinction rate histories that have the same likelihood. They also show that, when model and/or parameter space is limited, the “infinite plausible histories” usually collapse down into a single best-supported diversification history. This is why for many methods that fit diversification rates, we can generally find a way to limit the models chosen to avoid the identifiability problem.

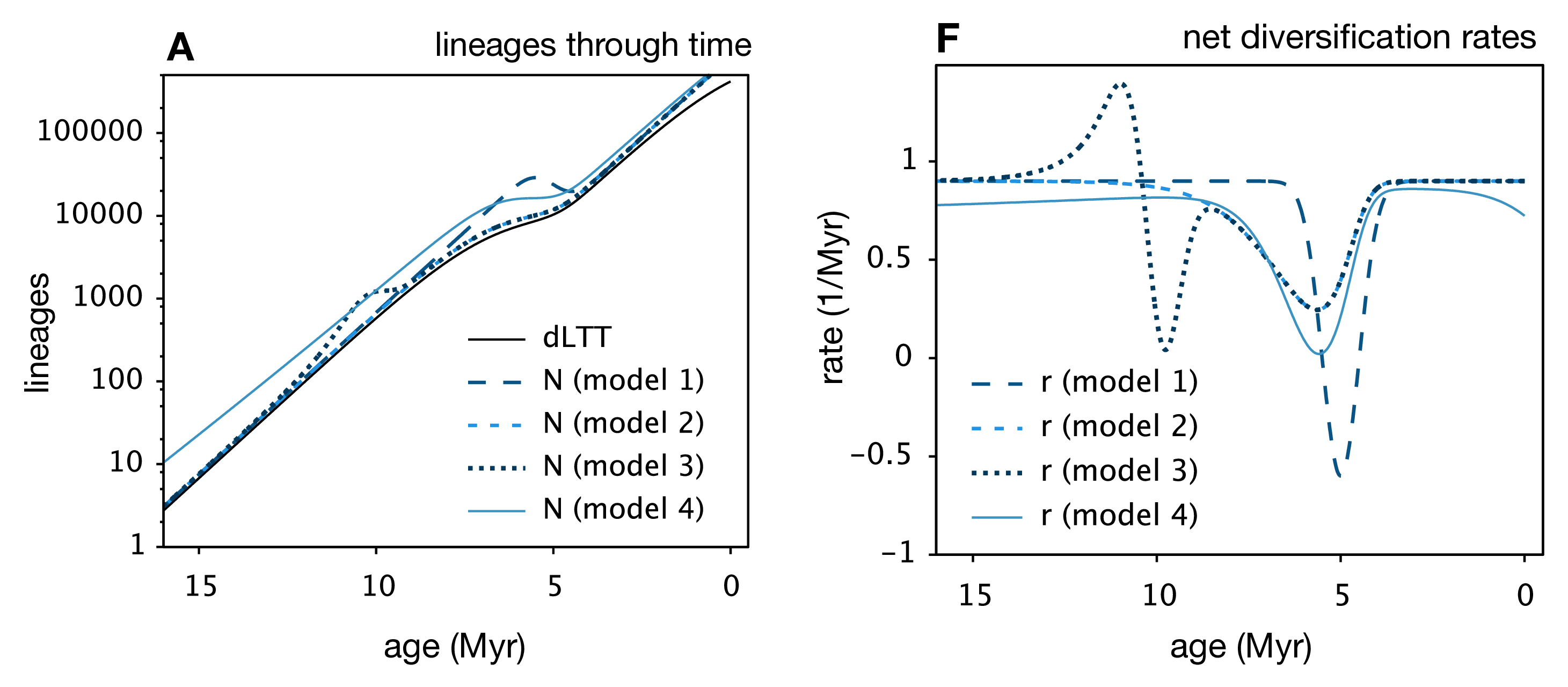
Many extensions to the general birth-death model are likely also affected by these results. We know from the Stadler paper⁵ that incomplete sampling can be non-identifiable, but I think this finding is fully general to many other extensions of the birth-death model, such as the birth-death-preservation model used for fossil phylogenies. In that case, we can estimate extinction due to the presence of extinct lineages, but varying extinction and preservation rates also lead to a non-identifiable model.⁷

In light of this paper, I think there’s a strong argument against trying to estimate a single true diversification history. For example, BAMM suggests using model averaging to summarize your posterior distribution of rate shift data, rather than just giving you a point estimate of the “best-supported” event configuration. Model averaging has also been shown to be quite good for SSE-class models, as pointed out in a recent paper.⁸

I also suspect that identifiability is the reason why, when simulating trees, the maximum likelihood estimate of that tree’s speciation and extinction rates don’t always match the generating parameters. There are a number of known pitfalls when simulating phylogenies,⁹ and our conditioning of the likelihood function can similarly mislead us,⁵ but it would be interesting to see if the results from this paper could be used to somehow improve the simulation of phylogenies as well.

Finally, I think these results suggest that the way we construct our models (e.g., assuming constant extinction), or impose our priors for Bayesian models, are going to remain important for breaking ties along the flat parts in parameter space. There will always be a ridge on the likelihood surface if you permit all possible models and areas of parameter space, so when analyzing diversification rates, practitioners should always consider how to encode assumptions and biological knowledge into our diversification rate models, and justifying those assumptions and priors adequately.

With all of the papers identifying the weaknesses of common analysis methods, it is easy to be discouraged about the state of comparative methods. I still recall the deep sense of despair at the first standalone Systematic Biology meeting in Ann Arbor, shortly after the Raboksy and Goldberg² manuscript was published and frightened the attendees into worrying whether we could do inference on phylogenies at all. I don’t think the alarmism and despair is really warranted, because as long as we are careful with how we analyze our data, justify the assumptions that are encoded into our models, and test for areas where our methods can be misleading, there is plenty of room to do great work with comparative methods.

¹⁰

References

1. Louca, S. and Pennell, MW. (2020). Extant timetrees are consistent with a myriad of diversification histories. Nature. doi:10.1038/s41586-020-2176-1 ↩

2. Rabosky, D. L., & Goldberg, E. E. (2015). Model Inadequacy and Mistaken Inferences of Trait-Dependent Speciation. Systematic Biology, 64(2), 340–355. doi:10.1093/sysbio/syu131 ↩

3. Nee, S., May, R. M., & Harvey. P.H. (1994). The reconstructed evolutionary process. Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences, 344(1309), 305–311. doi:10.1098/rstb.1994.0068 ↩

4. Rabosky, D. L. (2009). Extinction rates should not be estimated from molecular phylogenies. Evolution, 64(6), 1816–1824. doi:10.1111/j.1558-5646.2009.00926.x ↩

5. Stadler, T. (2012). How Can We Improve Accuracy of Macroevolutionary Rate Estimates? Systematic Biology, 62(2), 321–329. doi:10.1093/sysbio/sys073 ↩

6. Burin, G., Alencar, L. R. V., Chang, J., Alfaro, M. E., & Quental, T. B. (2018). How Well Can We Estimate Diversity Dynamics for Clades in Diversity Decline? Systematic Biology, 68(1), 47–62. doi:10.1093/sysbio/syy037 ↩

7. Foote, M., Sadler, P. M., Cooper, R. A., & Crampton, J. S. (2019). Completeness of the known graptoloid palaeontological record. Journal of the Geological Society, jgs2019–061. doi:10.1144/jgs2019-061 ↩

8. Caetano, D. S., O’Meara, B. C., & Beaulieu, J. M. (2018). Hidden state models improve state-dependent diversification approaches, including biogeographical models. Evolution, 72(11), 2308–2324. doi:10.1111/evo.13602 ↩

9. Hartmann, K., Wong, D., & Stadler, T. (2010). Sampling Trees from Evolutionary Models. Systematic Biology, 59(4), 465–476. doi:10.1093/sysbio/syq026 ↩

10. Thanks to James Saulsbury and Tomomi Parins-Fukuchi for suggestions that improved this blog post! ↩